2. Definition of 1D Asynchronous Cellular Automata
Wolfram [Wol 84] analyzes a type of one-dimensional cellular automata. Time is discrete in this model. The state of each cell is determined by the states of itself and the two neighbor cells in the previous time step. Wolfram's model is synchronous, as same as most other models. The states of all the cells are changed at the same time. However, an asynchronous model, which is called 1D-ACA, is used in the present paper. Many variations of asynchronous cellular automata can be devised, but a basically sequential model, which has similarity to the asynchronous Hopfield neural networks, is used in the present paper because it is easier to be analyzed.
1D-ACA is defined as follows (See the figure below). The state of i-th cell at time t is binary and expressed as s(i; t) (i.e., k = 2, or s(i; t) is 0 or 1). The initial states of cells, s(i; 0), are given, and the state of a cell is computed from the previous states of itself and two neighbor cells (i.e., r = 1) using the following rule when t > 0.
- s(i; t) = f(s(i - 1; t - 1), s(i; t - 1), s(i + 1; t - 1)) when i = ic(t), and
s(i; t) = s(i; t - 1) when i /= ic(t),
-
where s(-1; t) = s(N - 1; t) and s(N; t) = s(0; t)
(periodic boundary condition holds.)
(i = 0, 1, ..., N - 1, and t = 1, 2, ...).
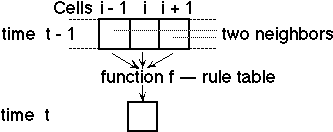
Figure . A state transition in 1D-ACA
Function f is mentioned later. State transitions are sequential, i.e., for each time step t, the state of only one cell, the ic(t)-th cell, (i.e., s(ic(t); t)) is updated. Condition s(i; t) = s(i; t - 1) holds for all other values of i. The order of computation, i.e., sequence ic(1), ic(2), ... (0 <= ic(1), ic(2), ... < N ) is defined by one of the following three methods.
- Random order: The elements of the sequence are uniform random numbers between 0 and N - 1.
- Fixed random order: The first N elements of the sequence are uniform random numbers, and these values are repeated in the sequence. Thus, the sequence is periodic. This order is used only in Section 5.
- Interlaced order: ic(t) = C t mod N, where C is an integral parameter and prime to N (gcd(C, N) = 1).
Interlaced orders have the maximum possible parallelism when C = ceiling((N - 1) / 2) or |_(N + 1) / 2_|. An example of interlaced orders is shown in Figure 2. The computation order in parity filter automata [Par 86] (i.e., left-to-right order) is the simplest interlaced order. Cells 0, 3 and 6 can be computed in parallel (i.e., the parallel computation makes no difference in the results), and cells 1, 4 and 7 can be computed in parallel in the next step, and so on.
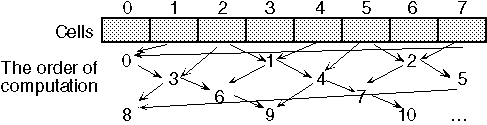
Figure 2. An example of interlaced orders (N = 8, C = 3)
Function f is defined using eight parameters or look-up table elements, the values of f0 = f(0, 0, 0), f1 = f(0, 0, 1), f2 = f(0, 1, 0), ..., f7 = f(1, 1, 1). This table can be regarded as a set of genes, or a chromosome. The genes determine the behavior of, or the patterns generated by the automata. An automaton is identified using eight-digit binary number f7 f6 f5 f4 f3 f2 f1 f0 [Wol 84]. For example, the identifier is #3 (in decimal) if the table elements are 1, 1, 0, 0, 0, 0, 0, 0.
Go to: Next section, Parent node
Y. Kanada

